resultant displacement|resultant displacement vector : Bacolod This physics video tutorial explains how to find the magnitude and direction of the resultant displacement vector. This video also explains how to add vectors analytically in component . * Save £117.00 off the monthly rate! * All 6 Football Trading Clubs! * Bonus In-Play Bets
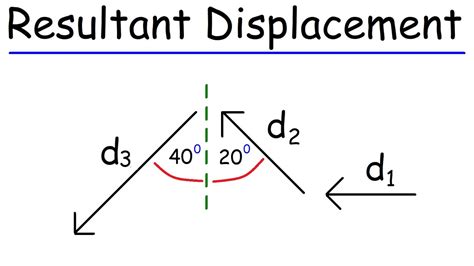
resultant displacement,This physics video tutorial explains how to find the magnitude and direction of the resultant displacement vector. This video also explains how to add vectors analytically in component .resultant displacementLearn how to add and subtract vectors using graphical methods, such as the parallelogram rule and the triangle rule. Find the resultant displacement of a vector by drawing a .resultant displacement resultant displacement vectorLearn how to add and subtract vectors using graphical methods, such as the parallelogram rule and the triangle rule. Find the resultant displacement of a vector by drawing a .
The resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together. If displacement vectors A, B, and C are added together, the result will . Calculate the velocity vector given the position vector as a function of time. Calculate the average velocity in multiple dimensions. Displacement and velocity in two .The resultant displacement is the hypotenuse of a right triangle that has sides 12 m, West and 16 m, South (from 28 m, South + 12 m, North). The Pythagorean theorem can be used to determine the magnitude of the . Resultant displacement (or total displacement) can be solved using 3 different methods: graphically, component method, and trigonometric method. Which one is.Learn how to use vector algebra to find resultant vectors and solve vector equations for unknown vectors. See examples of physical situations involving resultant displacement, .
Learn how to add and subtract vectors using graphical methods, such as the head-to-tail method and the tail-to-head method. Find out how to calculate the resultant .resultant displacement vector Subscribe Now:http://www.youtube.com/subscription_center?add_user=ehoweducationWatch More:http://www.youtube.com/ehoweducationFinding resultant displacement .The head-to-tail method outlined above will give a way to determine the magnitude and direction of the resultant displacement, denoted R R. Solution (1) Draw the three displacement vectors. Figure 3.14 (2) Place the vectors head to tail retaining both their initial magnitude and direction. Figure 3.15 Finding the Resultant of Two Displacements. We can use vectors to find direction, velocity, and force of moving objects. In this section we will look at a few applications where we will use resultants of vectors to find speed, direction, and other quantities. A displacement is a distance considered as a vector. Suppose, for example, that A is the vector representing the total displacement of the person walking in a city considered in Kinematics in Two Dimensions: . are two legs of a walk, and \(\displaystyle R\) is the resultant or total displacement. You can use analytical methods to determine the magnitude and direction of \(\displaystyle R\).The result (or resultant) of walking 11 km north and 11 km east is a vector directed northeast as shown in the diagram to the right. Since the northward displacement and the eastward displacement are at right angles to each other, the Pythagorean theorem can be used to determine the resultant (i.e., the hypotenuse of the right triangle).The resultant displacement is the vector sum of the two displacements experienced during the trip. Since they're perpendicular to one another, the resultant is the hypotenuse of a right triangle. Its magnitude can be found using pythagorean theorem and its direction can be found using the tangent function.The horizontal displacement of the projectile is called the range of the projectile and depends on the initial velocity of the object. . Resultant force on Earth’s surface, of the attraction by the Earth’s masses, and the centrifugal pseudo .Resultant displacement and vector addition have various real-life applications in mathematics education. One example is in navigation, where the resultant displacement can be used to determine the shortest distance between two points or to calculate the direction and magnitude of a ship or airplane's movement. Another application is in .

Displacement Formula. Displacement is calculated as the shortest distance between starting and final point which prefers straight-line path over curved paths. Suppose a body is moving in two different directions x and y then Resultant Displacement will be. It gives the shortcut paths for the given original paths. Here, u = Initial velocity The displacement is 10.3 blocks at an angle .1 º north of east. Figure graphically, draw an arrow to represent the total displacement vector \(D\). Using a protractor, draw a line at an angle \(θ\) relative to the east-west axis. The length \(D\) of the arrow is proportional to the vector’s magnitude and is measured along the line with a ruler.

The resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together. If displacement vectors A, B, and C are added together, the result will be vector R. As shown in the diagram, vector R can be determined by the use of an accurately drawn, scaled, vector addition diagram.. To say that vector R is the resultant .Figure 3.28 Vectors A A and B B are two legs of a walk, and R R is the resultant or total displacement. You can use analytical methods to determine the magnitude and direction of R R. If A A and B B represent two legs of a walk (two displacements), then R .The Principle of Superposition. The principle of superposition states that: When two or more waves meet, the resultant displacement is the vector sum of the displacements of the individual waves. This principle describes how waves which meet at a point in space interact. When two waves with the same frequency and amplitude arrive at a point .
The resultant displacement is the vector d, the sum of two vectors d 1 and d 2 which point in opposite directions. Details of the calculation: The sum of the two displacement vectors is d = d 1 + d 1 = (-110 m) + 25 . The resultant displacement formula is used when the distance from the point of reference is used to specify the initial and final position of the object. Despite the fact that distance and displacement are not the same things, displacement problems will tell you how many “foot” or “meters” an object has travelled. Problems would also . To find the magnitude of the resultant displacement, we can treat the student's movements as vectors and use vector addition. The displacement in the east direction is a vector of +1.0 kilometers, the displacement in the south direction is a vector of -1.0 kilometers, and the displacement in the west direction is a vector of -2.0 kilometers.
Resultant displacement (or total displacement) can be solved using 3 different methods: graphically, component method, and trigonometric method. Which one is.The resultant displacement is the vector d, the sum of two vectors d 1 and d 2 which point in opposite directions. Details of the calculation: Thee sum of the two displacement vectors is d = d 1 + d 1 = (-110 m) + 25 m = -85 m. You can also argue in the following way. For the total displacement it only matters where you start and where you stop.
resultant displacement|resultant displacement vector
PH0 · resultant displacement vector
PH1 · resultant displacement physics
PH2 · resultant displacement formula
PH3 · resultant displacement definition
PH4 · resultant displacement calculator
PH5 · formula to find displacement
PH6 · calculate total displacement
PH7 · calculate displacement
PH8 · Iba pa